
Cálculo
Imagina poder predecir el movimiento de los planetas, diseñar puentes indestructibles o comprender cómo crecen las poblaciones. Todo esto es posible gracias al cálculo, una de las herramientas más poderosas jamás creadas.
El cálculo nos permite analizar el cambio y la continuidad en el mundo. Con la derivada, podemos entender la velocidad y la aceleración, mientras que la integral nos ayuda a medir áreas, volúmenes y acumulaciones de cualquier tipo. Gracias a él, la ciencia y la tecnología han logrado avances impresionantes, desde la física hasta la inteligencia artificial.
Cada ecuación de cálculo es un puente entre lo abstracto y lo real, una clave para descifrar los patrones del universo. Dominarlo es como obtener un superpoder matemático que te permite explorar lo infinito y modelar el futuro.
¿Por qué es importante el Cálculo?
El cálculo es la base de la ciencia y la ingeniería modernas. Sin él, no tendríamos computadoras, naves espaciales, economía avanzada ni modelos climáticos precisos. Nos permite entender el mundo en términos de cambio y optimización, ayudándonos a resolver problemas complejos con aplicaciones en medicina, robótica y hasta inteligencia artificial. Aprender cálculo es desarrollar la capacidad de ver más allá de lo evidente y dar forma al futuro.


"El cálculo es la herramienta con la que desciframos el cambio, dominamos el infinito y modelamos el universo. 🔢✨"
Cálculo
La Matemática del Cambio y el Infinito






Temas con mayor dificultad de Aprendizaje en Cálculo
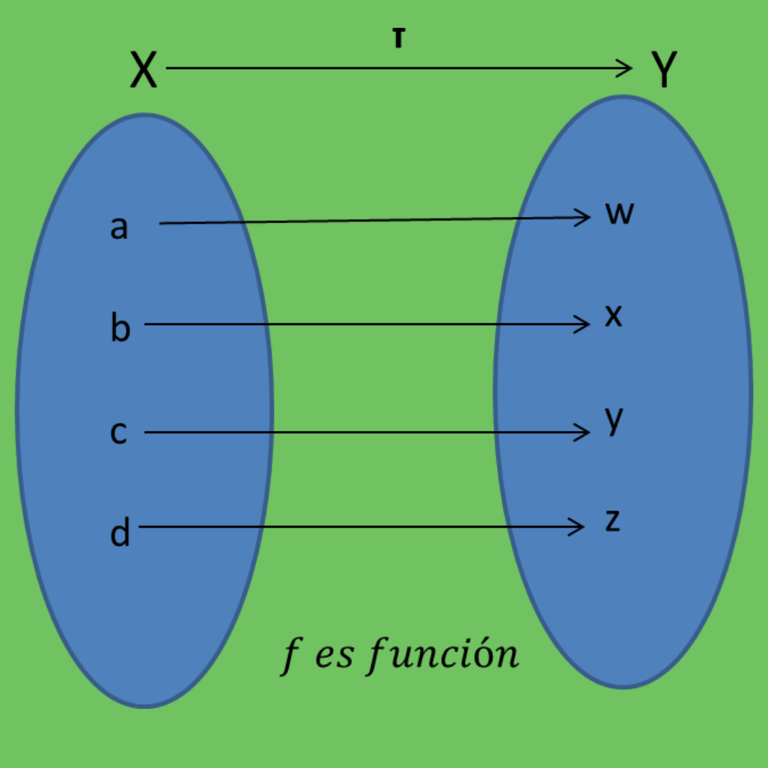
Concepto de Funcion
Cálculo de Límites
Derivación
Optimización y Extremos
Problemas de Aplicación
Series y Sucesiones
Cálculo de Integrales
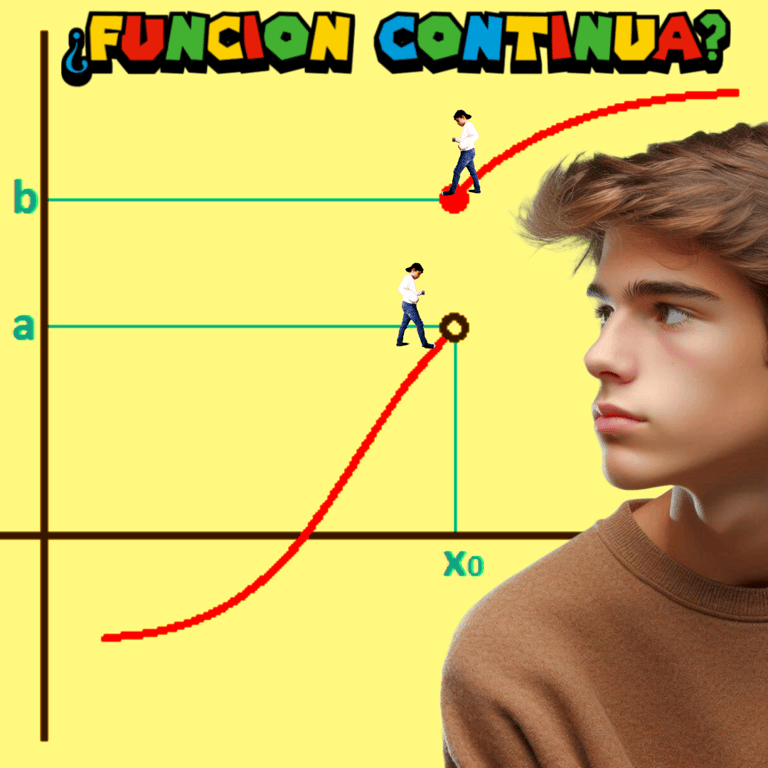
Noción de Continuidad
Dominio y Rango
Lo que suele suceder...
Al parecer la sola palabra Cálculo aterroriza a mas de uno, entonces de entrada ya hay una predisposición al tema. Para completar, los pocos fundamentos previos al Cálculo como son el correcto manejo de la Aritmética, el Álgebra y la Trigonometría ponen las cosas más complicadas...
Lo increíble es que los conceptos de cálculo aunque un poco abstractos no son en realidad difíciles de entender, todo el lío está en la situación previa a la materia en cuestión.
Solución de Ecuaciones Lineales
¿En verdad te enredas con ellas?
No mas que juegues a pasar las cosas de un lado hacia otro y estás listo!

Los temidos casos de Factorización
Es más el susto que pueden producir, que lo difícil que realmente son estos casos de factorización, vamos con toda!



Ecuaciones Cuadráticas
Después que sabes factorizar, esto de las cuadráticas es un verdadero paseo...

Inecuaciones
Si ya estás al día con las Ecuaciones, entonces no tienes por que preocuparte por esto de las Inecuaciones o Desigualdades Algebraicas, ya tienes mas de la mitad de lo que necesitas para entenderlas


Operaciones con Fracciones
Por todo lado hay fracciones hay de ti si no las comprendes




Temas con mayor dificultad de Aprendizaje en Trigonometria
En cálculo, los estudiantes suelen enfrentar dificultades en los siguientes temas:
1. Límites y continuidad
Comprender el concepto de límite y su interpretación gráfica.
Evaluación de límites que involucran indeterminaciones como 00\frac{0}{0} o ∞−∞\infty - \infty.
Definición formal de límite (ϵ−δ\epsilon - \delta).
2. Derivadas y sus aplicaciones
Interpretación geométrica y física de la derivada.
Regla de la cadena y derivadas implícitas.
Problemas de optimización y tasas relacionadas.
3. Integrales y técnicas de integración
Comprender la integral como el área bajo la curva.
Integrales indefinidas y definidas.
Métodos de integración: por partes, sustitución trigonométrica y fracciones parciales.
4. Series y sucesiones
Criterios de convergencia para series infinitas.
Series de Taylor y Maclaurin.
Comprender el concepto de aproximación mediante polinomios.
5. Ecuaciones diferenciales
Resolver ecuaciones diferenciales de primer orden.
Interpretación y aplicación en modelos físicos y biológicos.
6. Cálculo multivariable
Derivadas parciales y gradiente.
Integrales dobles y triples en coordenadas polares, cilíndricas y esféricas.
Campos vectoriales y teoremas fundamentales (Green, Stokes y Gauss).
7. Aplicaciones del cálculo
Modelado de fenómenos físicos y económicos.
Uso del cálculo en la inteligencia artificial y la ingeniería.
¿Quieres que me enfoque en algún tema específico para explicarlo mejor?
Ten especial cuidado con estos temas
Las siguientes temáticas son aquellas en las cuales se presentan mayores dificultades en el aprendizaje de los niños. Desafortunadamente todas estas temáticas son determinantes en la Aritmética y preceden el aprendizaje del Álgebra y por consiguiente todas las demás áreas de la matemáticas
Lo que suele suceder...
A veces el exceso de confianza de que "Aún queda tiempo para ponernos al día, el siguiente año será" o lo contrario, el miedo y la sensación de que las matemáticas son complicadas genera el ambiente perfecto para que los niños poco a poco vayan acumulando debilidades en la Aritmética y sin darsen cuenta, un día ya se vuelve muy complicado subsanar todos estos problemas.
Durante todos estos grados la Matemática se presenta de forma lineal, de modo que quedar con debilidades en el camino significa con seguridad tener serios problemas en el futuro y peor aún, el Álgebra se acerca cada vez más y allí las debilidades aritméticas causan grandes problemas en los estudiantes.








