
Universidad
Imagina poder modelar el flujo de un río, diseñar un avión que cruce océanos o desarrollar algoritmos que procesen señales en tiempo real. Todo esto es posible gracias a las matemáticas universitarias, el conjunto de herramientas avanzadas que forman el núcleo de la ingeniería moderna.
Las ecuaciones diferenciales nos permiten describir sistemas dinámicos: desde la propagación del calor hasta el movimiento de un satélite. El cálculo multivariado amplía la visión del cálculo a múltiples dimensiones, fundamental para optimizar procesos y comprender fenómenos complejos.
El álgebra lineal es el lenguaje de los vectores y matrices, clave en la computación, el diseño estructural y la inteligencia artificial.
Las transformadas de Fourier y Laplace son los instrumentos que nos permiten traducir problemas difíciles en representaciones más simples, esenciales para el análisis de señales, el control de sistemas y las telecomunicaciones.
Cada una de estas ramas no es solo teoría: son herramientas concretas que los ingenieros utilizan día a día para construir puentes, desarrollar tecnologías y resolver problemas que transforman la sociedad.
¿Por qué son importantes las Matemáticas Universitarias?
Porque son la base del pensamiento ingenieril. Permiten crear modelos precisos de la realidad, optimizar recursos, predecir comportamientos y diseñar soluciones innovadoras. Desde la electrónica hasta la aeronáutica, desde la informática hasta la biomedicina, ninguna rama de la ingeniería podría existir sin estas matemáticas avanzadas.


"Las matemáticas universitarias son el motor invisible de la ingeniería: transforman ecuaciones en puentes, algoritmos en tecnología y teoría en futuro. ⚙️📐✨"
Matemáticas Universitarias
El Lenguaje de la Ingeniería y la Innovación





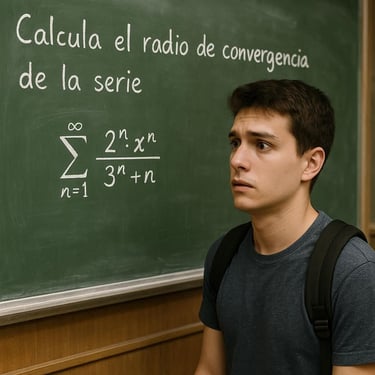


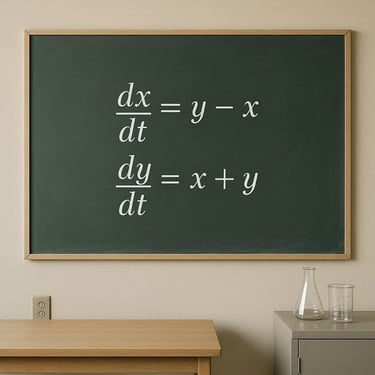
Temas con mayor dificultad de Aprendizaje en Matemáticas Universitarias
Concepto de Funcion
Cálculo de Límites
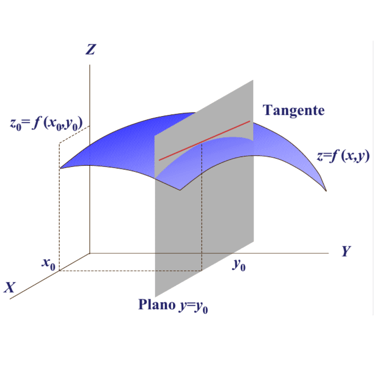
Derivadas Parciales
Optimización y Extremos
Series de Potencias
Integrales y Aplicaciones
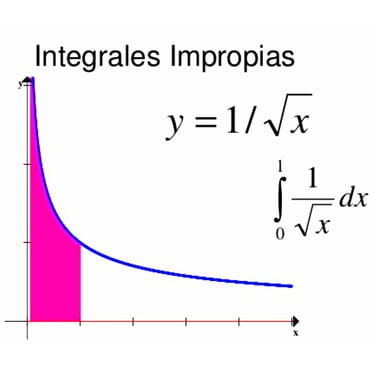
Integrales Impropias
Dominio y Rango
Ecuaciones Diferenciales
Transformada de Laplace
Sistemas de ED
Series y Transformada de Fourier
Lo que suele suceder...
Al parecer la sola palabra Cálculo aterroriza a mas de uno, entonces de entrada ya hay una predisposición al tema. Para completar, los pocos fundamentos previos al Cálculo como son el correcto manejo de la Aritmética, el Álgebra y la Trigonometría ponen las cosas más complicadas...
Lo increíble es que los conceptos de cálculo aunque un poco abstractos no son en realidad difíciles de entender, todo el lío está en la situación previa a la materia en cuestión.
Solución de Ecuaciones Lineales
¿En verdad te enredas con ellas?
No mas que juegues a pasar las cosas de un lado hacia otro y estás listo!

Los temidos casos de Factorización
Es más el susto que pueden producir, que lo difícil que realmente son estos casos de factorización, vamos con toda!



Ecuaciones Cuadráticas
Después que sabes factorizar, esto de las cuadráticas es un verdadero paseo...

Inecuaciones
Si ya estás al día con las Ecuaciones, entonces no tienes por que preocuparte por esto de las Inecuaciones o Desigualdades Algebraicas, ya tienes mas de la mitad de lo que necesitas para entenderlas


Operaciones con Fracciones
Por todo lado hay fracciones hay de ti si no las comprendes




Temas con mayor dificultad de Aprendizaje en Trigonometria
Cálculo Diferencial e Integral
Límites y continuidad en casos indeterminados → dificultad al aplicar correctamente reglas como L’Hôpital.
Integrales impropias → manejar infinitos y convergencia de áreas infinitas.
Series infinitas y pruebas de convergencia → especialmente las series de potencias y su radio de convergencia.
📗 Ecuaciones Diferenciales (Métodos y Laplace)
Ecuaciones diferenciales de segundo orden con coeficientes variables → difíciles por la falta de un método general directo.
Sistemas de ecuaciones diferenciales → trabajar con soluciones vectoriales y matrices.
Transformada de Laplace en problemas con funciones discontinuas (función escalón y delta de Dirac) → suele ser un reto conceptual y técnico.
📙 Cálculo Multivariado
Derivadas parciales y diferenciabilidad → confusión entre continuidad, existencia de derivadas y diferenciabilidad real.
Teoremas de Green, Stokes y Gauss → aplicar integrales múltiples y de línea/superficie correctamente.
Optimización con restricciones (método de Lagrange) → dificultad en interpretar y resolver sistemas de ecuaciones simultáneas.
📕 Transformada de Fourier
Series de Fourier y convergencia puntual/uniforme → entender cómo una función discontinua puede representarse por senos y cosenos.
Transformada de Fourier en señales no periódicas → abstracción al pasar de series a integrales.
Aplicaciones en resolución de EDO/PDE → dificultad en ver la conexión entre la transformada y la simplificación de un problema diferencial complejo.
Ten especial cuidado con estos temas
Las siguientes temáticas son aquellas en las cuales se presentan mayores dificultades en el aprendizaje de los niños. Desafortunadamente todas estas temáticas son determinantes en la Aritmética y preceden el aprendizaje del Álgebra y por consiguiente todas las demás áreas de la matemáticas
Lo que suele suceder...
A veces el exceso de confianza de que "Aún queda tiempo para ponernos al día, el siguiente año será" o lo contrario, el miedo y la sensación de que las matemáticas son complicadas genera el ambiente perfecto para que los niños poco a poco vayan acumulando debilidades en la Aritmética y sin darsen cuenta, un día ya se vuelve muy complicado subsanar todos estos problemas.
Durante todos estos grados la Matemática se presenta de forma lineal, de modo que quedar con debilidades en el camino significa con seguridad tener serios problemas en el futuro y peor aún, el Álgebra se acerca cada vez más y allí las debilidades aritméticas causan grandes problemas en los estudiantes.
