
Geometría y Estadística
Imagina poder diseñar edificios imponentes que se mantengan firmes por siglos y, al mismo tiempo, analizar millones de datos para descubrir tendencias ocultas. Eso es lo que nos ofrecen la geometría y la estadística: dos ramas de la matemática que, aunque distintas, se complementan para entender el mundo en su forma y en su comportamiento.
La geometría nos enseña a comprender el espacio, las proporciones y las formas que nos rodean. Gracias a ella medimos distancias, áreas y volúmenes, construimos puentes, exploramos planetas y damos forma a nuestras ciudades.
La estadística, en cambio, nos da el poder de interpretar la información que produce la realidad. Con ella podemos analizar encuestas, entender fenómenos sociales, estudiar la probabilidad de un evento o anticipar el futuro a partir de los datos.
Cada figura geométrica revela un orden en el espacio, y cada gráfico estadístico nos cuenta una historia sobre cómo cambia el mundo. Juntas, forman un puente entre lo visible y lo cuantitativo, entre lo que podemos ver y lo que podemos predecir.
¿Por qué son importantes la Geometría y la Estadística?
Sin la geometría no tendríamos arquitectura, navegación, robótica ni exploración espacial. Sin la estadística, la ciencia moderna sería ciega frente a los datos: no podríamos entender la economía, la medicina, la inteligencia artificial ni el comportamiento de la sociedad. Aprender ambas es adquirir la capacidad de visualizar y analizar, de construir y anticipar, de dar forma y sentido a la realidad.
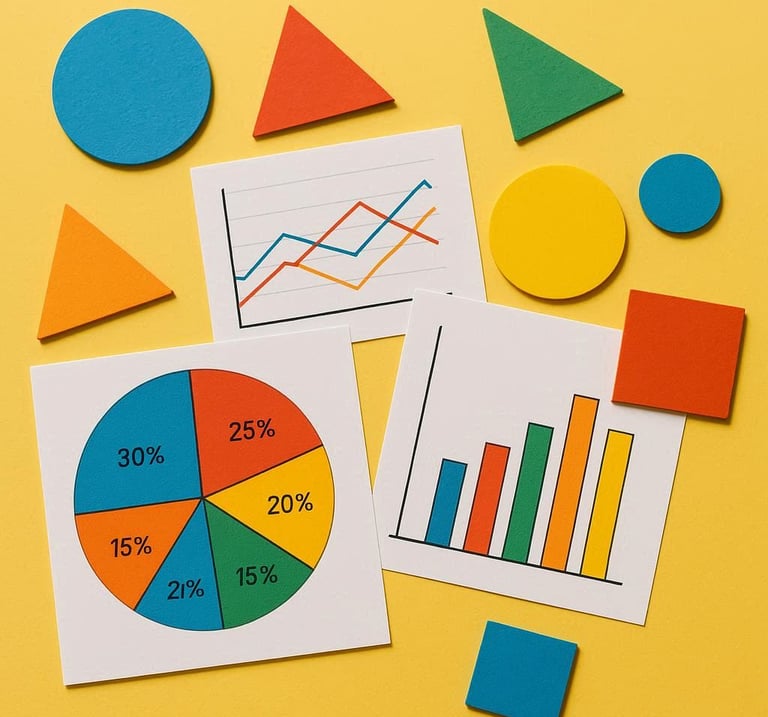
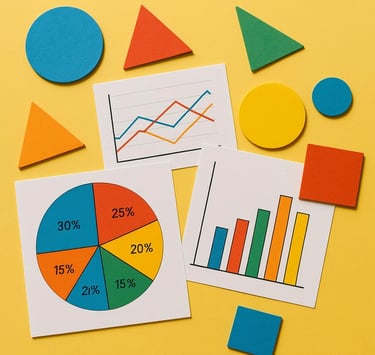
"La geometría y la estadística son los lentes con los que desciframos el espacio y los datos: nos permiten ver el orden en lo visible y predecir lo oculto. 📐📊✨"
Geometría y Estadística
Las Formas del Espacio y los Patrones de los Datos











Temas con mayor dificultad de Aprendizaje en Geometría y Estadística
Teorema de Pitágoras, Tales, Euclides
Polígonos
Distribución de Probabilidad
Prismas y Volumen
Problemas de Aplicación
Medidas de Dispersión
Regresiones
Calculo de Probabilidad
Noción de Ángulo y Medidas
Áreas y Perímetros
Transformaciones
Congruencia y Semejanza
Relaciones Angulares
Medidas de Tendencia Central
Análisis Gráfico
Lo que suele suceder...
El miedo generalizado a las matemáticas, el creer que son difíciles y complejas, se extiende a las ramas de la Geometría y la Estadística, y es entonces cuando las figuras geométricas parecen pesadas y sus teoremas aburridos y sin sentido, y la Estadística se enreda debido a las bases débiles en aritmética
El asunto es que con lo básico en aritmética y algo de álgebra, ya es posible llegar a ser muy bueno en Geometría y Estadística, por lo que todo es cuestión de dejar a un lado el miedo y la incomodidad y atreverse a ir con toda por estas increíbles áreas de la matemática
Solución de Ecuaciones Lineales
¿En verdad te enredas con ellas?
No mas que juegues a pasar las cosas de un lado hacia otro y estás listo!

Los temidos casos de Factorización
Es más el susto que pueden producir, que lo difícil que realmente son estos casos de factorización, vamos con toda!



Ecuaciones Cuadráticas
Después que sabes factorizar, esto de las cuadráticas es un verdadero paseo...

Inecuaciones
Si ya estás al día con las Ecuaciones, entonces no tienes por que preocuparte por esto de las Inecuaciones o Desigualdades Algebraicas, ya tienes mas de la mitad de lo que necesitas para entenderlas


Operaciones con Fracciones
Por todo lado hay fracciones hay de ti si no las comprendes




Temas con mayor dificultad de Aprendizaje en Trigonometria
En cálculo, los estudiantes suelen enfrentar dificultades en los siguientes temas:
1. Teoremas y demostraciones
Comprender y aplicar teoremas fundamentales como el de Pitágoras, Tales y Euclides.
Razonamiento lógico para demostrar propiedades geométricas.
2. Ángulos y paralelismo
Relación entre ángulos formados por líneas paralelas y una transversal.
Cálculo de ángulos en polígonos regulares e irregulares.
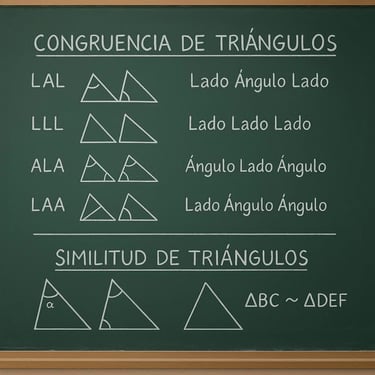
3. Triángulos y congruencia
Criterios de congruencia (LAL, LLL, ALA, etc.) y semejanza de triángulos.
Aplicaciones en problemas de medición indirecta.
4. Círculos y sus propiedades
Cuerdas, tangentes y secantes.
Ángulos inscritos y centrales, además de sus relaciones.
5. Áreas y volúmenes
Cálculo del área de figuras compuestas.
Volúmenes de prismas, cilindros, conos y esferas.
6. Coordenadas y geometría analítica
Ecuaciones de rectas, circunferencias y parábolas.
Distancia entre puntos, punto medio y pendiente de una recta.
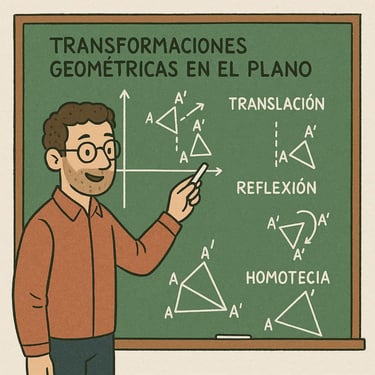
7. Transformaciones geométricas
Reflexiones, traslaciones, rotaciones y homotecias.
Comprensión de la simetría y el efecto de cada transformación.
Si quieres, puedo explicarte más a fondo algún tema o darte ejemplos prácticos.
Ten especial cuidado con estos temas
Las siguientes temáticas son aquellas en las cuales se presentan mayores dificultades en el aprendizaje de los niños. Desafortunadamente todas estas temáticas son determinantes en la Aritmética y preceden el aprendizaje del Álgebra y por consiguiente todas las demás áreas de la matemáticas
Lo que suele suceder...
A veces el exceso de confianza de que "Aún queda tiempo para ponernos al día, el siguiente año será" o lo contrario, el miedo y la sensación de que las matemáticas son complicadas genera el ambiente perfecto para que los niños poco a poco vayan acumulando debilidades en la Aritmética y sin darsen cuenta, un día ya se vuelve muy complicado subsanar todos estos problemas.
Durante todos estos grados la Matemática se presenta de forma lineal, de modo que quedar con debilidades en el camino significa con seguridad tener serios problemas en el futuro y peor aún, el Álgebra se acerca cada vez más y allí las debilidades aritméticas causan grandes problemas en los estudiantes.
En cálculo, los estudiantes suelen enfrentar dificultades en los siguientes temas:
1. Tipos de datos y representaciones gráficas
Diferenciar entre datos cualitativos y cuantitativos.
Interpretar y construir gráficos de barras, histogramas, diagramas de caja y gráficos circulares.
2. Medidas de tendencia central
Cálculo e interpretación de la media, mediana y moda en diferentes conjuntos de datos.
Diferencias entre estos valores y cuándo es más útil cada uno.
3. Medidas de dispersión
Cálculo del rango, varianza y desviación estándar.
Interpretación de la dispersión de datos en diferentes contextos.
4. Probabilidad y conteo
Reglas de la probabilidad (adición, multiplicación e independencia de eventos).
Espacios muestrales y diagramas de árbol.
5. Distribuciones de probabilidad
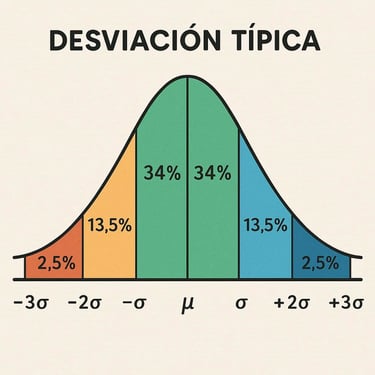
Comprender la distribución normal y su importancia.
Conceptos como la curva de campana y la regla empírica (68-95-99.7).
6. Correlación y regresión
Identificación de relaciones entre variables mediante diagramas de dispersión.
Interpretación del coeficiente de correlación y su significado.
7. Inferencia estadística (introducción)
Conceptos básicos de estimaciones y margen de error.
Comprender la importancia de las muestras y cómo afectan los resultados.
Si necesitas que explique un tema en particular o con ejemplos, dime cuál te interesa más. 😊
