
Trigonometría
Imagina un mundo sin trigonometría: sin navegación precisa, sin rascacielos imponentes, sin exploración espacial. La trigonometría es mucho más que números y fórmulas; es la clave para entender el mundo.
Desde la antigüedad, se ha usado para mapear estrellas, construir maravillas arquitectónicas y avanzar en la tecnología. Sus funciones, como el seno y coseno, describen desde el sonido hasta el movimiento de los planetas.
Cada triángulo que trazas conecta con siglos de descubrimientos. Dominar la trigonometría es hablar el lenguaje de la ciencia y la innovación.
¿Por qué es importante la trigonometría?
La trigonometría no es solo un tema académico, sino una herramienta esencial en la ciencia, la ingeniería, la astronomía y hasta en la tecnología moderna. Nos permite calcular distancias sin necesidad de medirlas directamente, entender el comportamiento de ondas como el sonido y la luz, y diseñar estructuras resistentes. Su aplicación está en todas partes: desde los sistemas GPS hasta la inteligencia artificial. Aprender trigonometría es abrir una puerta a un mundo de posibilidades.
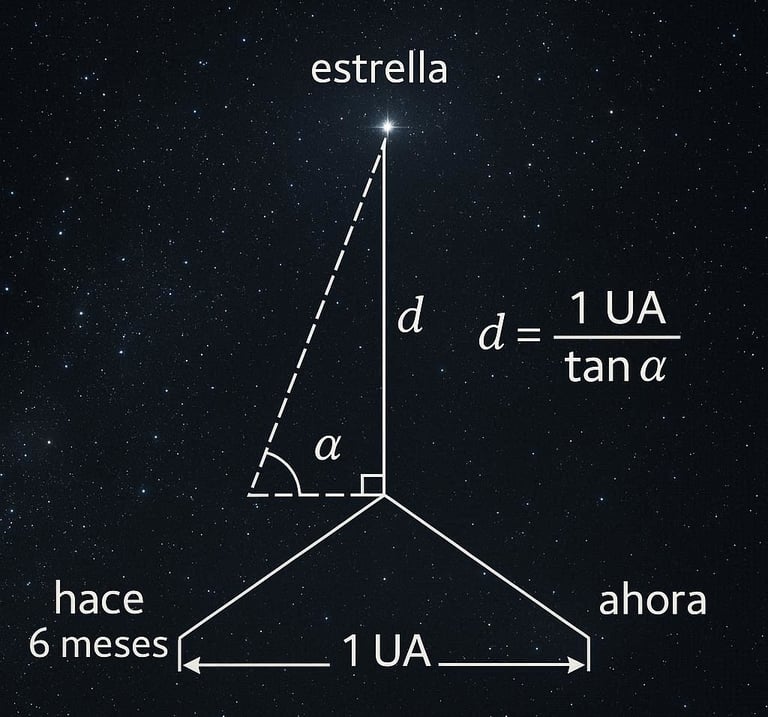
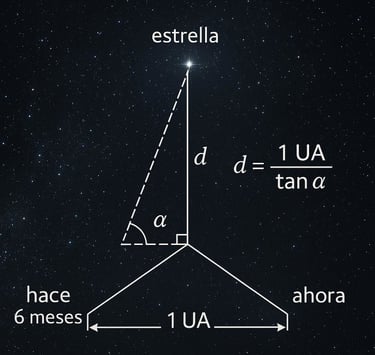
“La trigonometría es el lenguaje con el que medimos el cielo, exploramos el infinito y damos forma a lo imposible. ⭐✨”
Trigonometría
El Lenguaje de los Ángulos y las Estrellas


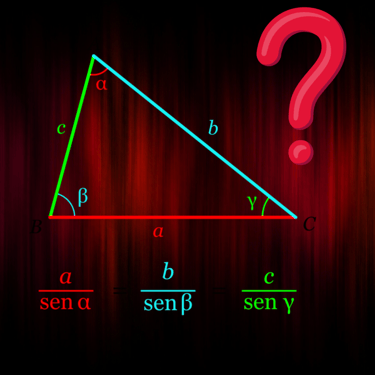



Temas con mayor dificultad de Aprendizaje en Trigonometría
Funciones
Trigonométricas
Medición de Ángulos
Identidades Trigonométricas
Ecuaciones Trigonométricas
Solución de Triángulos
Gráfica de Funciones T.
Ley de Senos y Cosenos
Resolución Problemas
Lo que suele suceder...
Piensas que ya pasaste todas esas matemáticas tediosas y complicadas y respiras con tranquilidad sabiendo que ya saliste de ello. Y ahora, aunque con un poco de temor con ese nombre tan raro y tal vez feo de la trigonometría, solo será cuestión de comenzar de nuevo y esta vez estar juicios@ con este nuevo tema.
Luego, en el camino te das cuenta que nuevamente tu gran debilidad son tus bases, lo de atrás, lo que debiste aprender sobre aritmética y álgebra, ahora estás de nuevo en problemas, y peor que antes
Solución de Ecuaciones Lineales
¿En verdad te enredas con ellas?
No mas que juegues a pasar las cosas de un lado hacia otro y estás listo!

Los temidos casos de Factorización
Es más el susto que pueden producir, que lo difícil que realmente son estos casos de factorización, vamos con toda!



Ecuaciones Cuadráticas
Después que sabes factorizar, esto de las cuadráticas es un verdadero paseo...

Inecuaciones
Si ya estás al día con las Ecuaciones, entonces no tienes por que preocuparte por esto de las Inecuaciones o Desigualdades Algebraicas, ya tienes mas de la mitad de lo que necesitas para entenderlas


Operaciones con Fracciones
Por todo lado hay fracciones hay de ti si no las comprendes




Temas con mayor dificultad de Aprendizaje en Trigonometria
En trigonometría, los temas que suelen presentar mayor dificultad para los estudiantes son los siguientes:
1. Razones trigonométricas y su interpretación
Dificultad para comprender la relación entre los lados de un triángulo y las funciones trigonométricas (seno, coseno, tangente, etc.).
Confusión con los valores de las razones en distintos cuadrantes.
2. Identidades trigonométricas
Memorización y demostración de identidades fundamentales como: sin2θ+cos2θ=1\sin^2\theta + \cos^2\theta = 1 1+tan2θ=sec2θ1 + \tan^2\theta = \sec^2\theta
Manipulación algebraica para demostrar o simplificar expresiones.
3. Resolución de triángulos
Uso de la ley de senos y la ley de cosenos en triángulos oblicuángulos.
Diferenciar cuándo aplicar cada ley según los datos dados.
4. Funciones trigonométricas y su gráfica
Interpretación de la amplitud, periodo y fase en funciones como f(x)=asin(bx+c)f(x) = a \sin(bx + c).
Transformaciones de las gráficas trigonométricas.
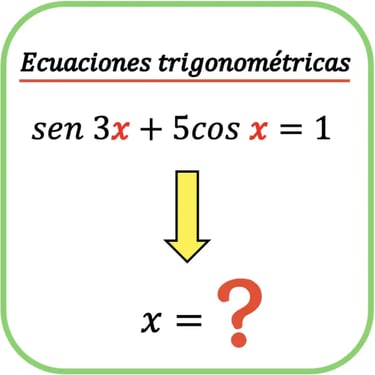
5. Ecuaciones trigonométricas
Resolución de ecuaciones en intervalos dados.
Manejo de soluciones múltiples en función del periodo de la función.
6. Ángulos y coordenadas en la circunferencia trigonométrica
Conversión entre radianes y grados.
Ubicación de ángulos en la circunferencia y determinación del signo de las razones trigonométricas.
7. Aplicaciones en problemas de la vida real
Uso de la trigonometría en navegación, construcción y física.
Planteo de problemas con razones trigonométricas.
¿En qué tema específico quieres enfocarte para explicarlo mejor?
Ten especial cuidado con estos temas
Las siguientes temáticas son aquellas en las cuales se presentan mayores dificultades en el aprendizaje de los niños. Desafortunadamente todas estas temáticas son determinantes en la Aritmética y preceden el aprendizaje del Álgebra y por consiguiente todas las demás áreas de la matemáticas
Lo que suele suceder...
A veces el exceso de confianza de que "Aún queda tiempo para ponernos al día, el siguiente año será" o lo contrario, el miedo y la sensación de que las matemáticas son complicadas genera el ambiente perfecto para que los niños poco a poco vayan acumulando debilidades en la Aritmética y sin darsen cuenta, un día ya se vuelve muy complicado subsanar todos estos problemas.
Durante todos estos grados la Matemática se presenta de forma lineal, de modo que quedar con debilidades en el camino significa con seguridad tener serios problemas en el futuro y peor aún, el Álgebra se acerca cada vez más y allí las debilidades aritméticas causan grandes problemas en los estudiantes.








